Zadowolony
W geometrii, po punkcie, linia prosta jest chyba najprostszym elementem. Znajduje zastosowanie w budowie wszelkich skomplikowanych kształtów na płaszczyźnie i w przestrzeni trójwymiarowej. W tym artykule przyjrzymy się ogólnemu równaniu linii prostej i rozwiążemy kilka problemów z jego użyciem. Zacznijmy!
Linia prosta w geometrii

Każdy wie, że figury takie jak prostokąt, trójkąt, graniastosłup, sześcian itp. powstają w wyniku przecięcia się linii prostych. Za linię prostą w geometrii uważa się obiekt jednowymiarowy, który można uzyskać przez przeniesienie określonego punktu na wektor mający ten sam lub przeciwny kierunek. Aby lepiej zrozumieć tę definicję, wyobraźmy sobie, że w przestrzeni istnieje punkt P. Weźmy dowolny wektor uŻ w tej przestrzeni. Wówczas dowolny punkt Q prostej można otrzymać jako wynik następujących operacji matematycznych:
Q = P + λ∗u¯.
Tutaj λ jest dowolną liczbą, która może być pozytywny i negatywny. Jeśli powyższą równość zapiszemy poprzez współrzędne, otrzymamy następujące równanie prostej
(x, y, z) = (x0, y0, z0) + λ∗(a, b, c).
Równanie to nazywamy równaniem linii prostej w postaci wektorowej. A wektor uŻ nazywany jest przewodnikiem.
Ogólne równanie linii prostej na płaszczyźnie
Każdy uczeń może ją bez trudu zapisać. Najczęściej jednak równanie zapisuje się tak:
y = k*x + b.
Gdzie k i b są dowolnymi liczbami. Liczba b jest nazywana wyrazem wolnym. Parametr k jest równy tangensowi kąta utworzonego przez przecięcie prostej z osią odciętych.
Dane równanie jest wyrażone w odniesieniu do zmiennej y. Jeśli przedstawi się ją w bardziej ogólnej formie, to mamy następującą formę zapisu:
A*x + B*y + C = 0.
Łatwo pokazać, że tę postać ogólnego równania prostej na płaszczyźnie można łatwo przekształcić w poprzednią postać. W tym celu należy podzielić lewą i prawą stronę przez czynnik B i wyrazić y.

Na rysunku powyżej przedstawiono prostą przechodzącą przez dwa punkty.
Linia prosta w trzech wymiarach
Kontynuujmy nasze badania. Rozważaliśmy, jak równanie prostej można podać na płaszczyźnie w postaci ogólnej. Jeśli zastosujemy formę notacji podaną w poprzednim punkcie pracy do przypadku przestrzennego, to otrzymamy? To proste - to już nie jest linia prosta, ale płaszczyzna. Rzeczywiście, poniższe wyrażenie opisuje płaszczyznę, która jest równoległa do osi z:
A*x + B*y + C = 0.
Jeżeli C=0, to płaszczyzna ta przechodzi przez oś z. Ważne jest funkcja.
A co z ogólnym równaniem linii prostej w przestrzeni? Aby zrozumieć jak go ustawić, musimy pamiętać o czymś. Dwie płaszczyzny przecinają się wzdłuż pewnej linii prostej. Co to znaczy? Tylko, że, co jest powszechne jest wynikiem rozwiązania układu dwóch równań dla płaszczyzn. Zapiszmy ten system:
- A1*x + B1*y + C1*z + D1= 0;
- A2*x + B2*y + C2*z + D2= 0.
Układ ten jest ogólnym równaniem linii prostej w przestrzeni. Należy pamiętać, że płaszczyzny nie mogą być do siebie równoległe, tzn. ich wektory normalne muszą być nachylone pod jakimś kątem względem siebie. W przeciwnym razie system nie będzie miał rozwiązań.

Powyżej podaliśmy wektorową postać równania linii prostej. Jest wygodny do stosowania przy rozwiązywaniu tego systemu. Aby to zrobić, należy najpierw znaleźć iloczyn wektorowy normaliów danych płaszczyzn. Wynikiem tej operacji jest wektor kierunkowy prostej. Następnie oblicz dowolny punkt należący do prostej. W tym celu należy umieścić dowolną ze zmiennych równą pewnej wartości, dwie pozostałe zmienne znajdziemy rozwiązując powyższy układ.
Jak przekształcić równanie wektorowe na równanie ogólne? Subtelności

Jest to rzeczywisty problem, który może się pojawić, jeśli ktoś miałby napisać ogólne równanie prostej, używając znanych współrzędnych dwóch punktów. Pokażmy, jak ten problem jest rozwiązany na następującym przykładzie. Niech znane będą współrzędne dwóch punktów:
- P = (x1, y1);
- Q = (x2, y2).
Możemy łatwo skonstruować to równanie w postaci wektorowej. Współrzędne wektora prowadzącego to:
PQ = (x2-x1, y2-y1).
Zauważ, że nie ma znaczenia, czy współrzędne P zostaną odjęte od współrzędnych Q, wektor zmieni tylko kierunek na przeciwny. Teraz weź dowolny punkt i zapisz równanie wektora:
(x, y ) = (x1, y1) + λ*(x2-x1, y2-y1).
Aby napisać ogólne równanie linii, należy w obu przypadkach wyrazić parametr λ. A potem zrównaj wyniki z. Mamy:
x = x1+ λ*(x2-x1) => λ = (x-x1)/(x2-x1);
y = y1+ λ*(y2-y1) => λ = (y-y1)/(y2-y1) =>
(x-x1)/(x2-x1) = (y-y1)/(y2-y1).
Pozostaje tylko otworzyć nawiasy i odwrócić wszystkie warunki równania na jedna strona równości, aby otrzymać ogólne wyrażenie na prostą przechodzącą przez dwa znane punkty.
W przypadku problemu trójwymiarowego algorytm rozwiązania pozostaje taki sam, tylko wynikiem będzie układ dwóch równań dla płaszczyzn.
Problem
Należy podać ogólne równanie prostej, która przecina oś x w punkcie (-3, 0) i która jest równoległa do osi y.
Rozwiązywanie zadania rozpoczynamy od zapisania równania w postaci wektorowej. Ponieważ prosta jest równoległa do osi rzędnych, wektor ją prowadzący będzie następujący:
u¯ = (0, 1).
Wtedy pożądana linia jest zapisana tym równaniem:
(x, y) = (-3, 0) + λ∗(0, 1).
Przekształćmy teraz to wyrażenie do postaci ogólnej poprzez wyrażenie parametru λ:
- x = -3;
- y = λ.
Zatem każda wartość y należy do linii, ale tylko jedna wartość x jej odpowiada. Zatem ogólne równanie przyjmie postać:
x + 3 = 0.
Problem z linią prostą w przestrzeni

Wiadomo, że dwie przecinające się płaszczyzny są dane następującymi równaniami:
- 2∗x + y - z = 0;
- x - 2*y + 3 = 0.
Potrzebowaliśmy znaleźć równanie wektora prostej, przez którą przecinają się te płaszczyzny. Zacznijmy.
Jak już powiedziano, ogólne równanie prostej w trzech wymiarach jest już dane jako układ dwóch z trzema niewiadomymi. Najpierw wyznaczmy wektor kierunkowy, wzdłuż którego przecinają się płaszczyzny. Mnożąc wektorowo współrzędne norm płaszczyzn otrzymujemy:
u¯ = [(2, 1, -1)*(1, -2, 0)] = (-2, -1, -5).
Ponieważ pomnożenie wektora przez liczbę ujemną zmienia jego kierunek na przeciwny, możemy napisać:
u¯ = -1*(-2, -1, -5) = (2, 1, 5).
Aby znaleźć wyrażenie wektorowe dla prostej, oprócz wektora prowadzącego musimy znać jakiś punkt prostej. Ponieważ jego współrzędne muszą spełniać układ równań zawarty w treści zadania, znajdujemy je. Niech x = 0 dla przykładu, wtedy otrzymamy
y = z;
y = 3/2 = 1,5.
Zatem punkt należący do szukanej prostej ma współrzędne
P = (0, 1,5, 1,5).
Otrzymujemy wtedy odpowiedź na to zagadnienie, równanie wektorowe szukanej prostej będzie miało postać:
(x, y, z) = (0, 1,5, 1,5) + λ∗(2, 1, 5).
Poprawność rozwiązania można łatwo sprawdzić. W tym celu wybieramy dowolną wartość parametru λ i otrzymane współrzędne punktu prostej podstawiamy do obu równań płaszczyzn, otrzymując w obu przypadkach tożsamość.
 Obliczanie kąta między prostą a płaszczyzną. Metoda współrzędnych w rozwiązywaniu problemów
Obliczanie kąta między prostą a płaszczyzną. Metoda współrzędnych w rozwiązywaniu problemów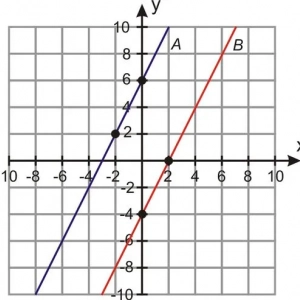 Odległość między prostymi równoległymi. Odległość między płaszczyznami równoległymi
Odległość między prostymi równoległymi. Odległość między płaszczyznami równoległymi Cechy percepcyjne: iluzje czasu i przestrzeni
Cechy percepcyjne: iluzje czasu i przestrzeni Jak narysować dzwoneczka krok po kroku. Oto ogólne wprowadzenie
Jak narysować dzwoneczka krok po kroku. Oto ogólne wprowadzenie Dieta lchf: recenzje, ogólne zasady żywienia, zalecane produkty spożywcze
Dieta lchf: recenzje, ogólne zasady żywienia, zalecane produkty spożywcze Jak narysować catwoman, punkty ogólne
Jak narysować catwoman, punkty ogólne Luka w linii życia na dłoni: znaczenie, niuanse rozszyfrowania za pomocą zdjęcia
Luka w linii życia na dłoni: znaczenie, niuanse rozszyfrowania za pomocą zdjęcia Przejście dla pieszych: szerokość i oznakowanie przejścia, ogólne wymagania dotyczące umieszczenia, zgodność z gost 32944-2014
Przejście dla pieszych: szerokość i oznakowanie przejścia, ogólne wymagania dotyczące umieszczenia, zgodność z gost 32944-2014 Projekt pokoju z przegrodą: ciekawe pomysły, strefowanie przestrzeni i dobre przykłady ze zdjęciami
Projekt pokoju z przegrodą: ciekawe pomysły, strefowanie przestrzeni i dobre przykłady ze zdjęciami